공개키 암호 개요
- 기존 대칭키 암호의 한계
- 기존 대칭키 암호 체계에서는 1:1 통신 마다 키가 필요하다
- 즉, n명 통신시에는 $\frac{n(n-1)}{2}$ 개의 키가 필요하다.
- 통신을 위해 항상 키를 가지고 있어야 한다.
- 키가 많아지면 오버헤드가 발생한다.
- 기존 대칭키 암호 체계에서는 1:1 통신 마다 키가 필요하다
Solution : 공개키 (비대칭키) 암호 시스템
공개키 (비대칭키) 암호 시스템
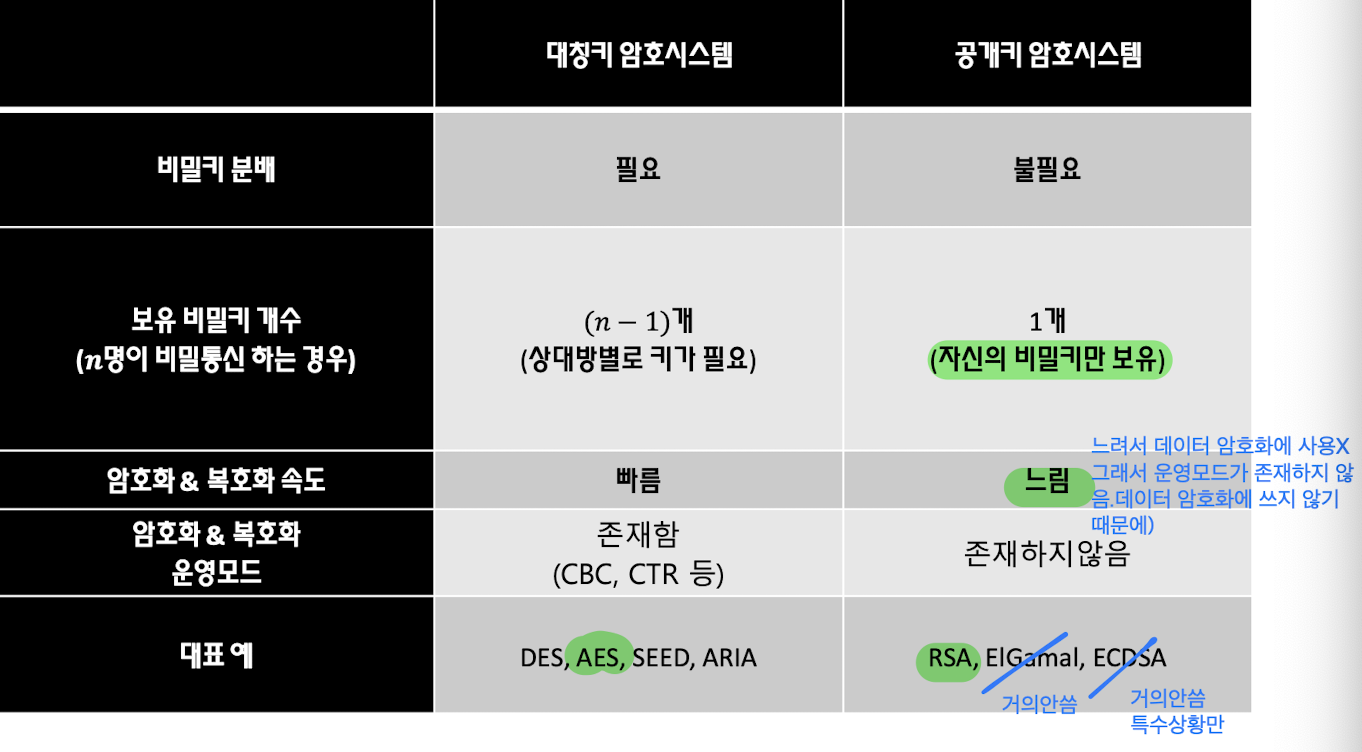
- Diffie, Hellman은 1976년 발표된 논문 *"New Directions in Cryptography"* 에서 공개키 암호 시스템을 소개한다.
- 각 사람마다 한 쌍의 키를 보유한다. (
공개키 pubkey,개인키 secret(private) key)- 공개키는 모두에게 공개되고, 개인키는 비밀로 보관한다.
- 공개키를 안다고 해서 이를 통해 개인키를 유추하는 것은 수학적으로 불가능하다.
RSA
대표적인 공개키 암호인 RSA에 대해 알아보자.
RSA Key Generation
- 소수 $p$ ,$q$를 생성한다.
- $n = p * q$ 계산
- $\phi(n) = \phi(p) * \phi(q) = (p - 1) * (q - 1)$
- 공개키 $e$ 선택 : $1 < e < \phi(n) - 1$ 을 만족하고, $\phi(n)$과 서로소인 관계
- 개인키 $d$ 계산 : $e * d \equiv 1 mod \phi(n)$
공개되는 값은 $e, n$이다.
비밀 값은 d 이다. (p, q 는 키 생성 후 삭제한다.)
공개된 값인 $e, n$으로부터 $d$를 구하려면?
- $\phi(n)$을 구해야 한다. -> 이는 어려운 일이다. (n 을 소인수 분해 해야하기 때문)
- $e * d \equiv 1 mod \phi(n)$ -> 간단한 일이다.
c.f.
$gcd(e,\phi(n)) = 1$ 를 만족하는 $e$를 뽑아야 한다.
근데 $\phi(n)$ = $\alpha$ * 65537 인 경우가 있을 수 있다. (아주 드물게)
이 경우를 방지하기 위해
- $(p-1) mod 4 = 2$
- $(q-1) mod 4 = 2$ 이런 테스트를 만족하게끔 $e$를 뽑는다!
$\phi$란?
오일러 파이 함수이다.
즉, $\phi(n)$는 "n과 서로소인 수의 개수" 라는 의미이다.
이 함수를 일반화하면 다음과 같다.
case 1 : $\phi(1)$ = 0
case p는 소수 : $\phi(p) = p-1
case m, n은 소수 : $\phi(m * n = \phi(m) * \phi(n)$
소인수 * 소인수 = 합성수이고,
아주 큰 합성수를 분해하는 과정은 매우 어렵고 복잡하다.
즉, 공격자 입장에서는 합성수 n을 알아도 이를 구성하는 소수인 p, q의 값을 알기가 매우 어렵다.
| 암복호화 예제
$c = m^e\ mod\ n$
$m = c^d\ mod\ n = (m^e)^d\ mod\ n = m^{e*d}\ mod\ n = m^1\ mod\ n$
$e, n로\ d알아내기?$
$e * d = 1\ (mod\ \phi(n))$
$\phi(n) = \phi(p)\phi(q) = (p-1)*(q-1)$
즉, n을 소인수 분해해야 한다.
소인수 분해 알고리즘은 아직 존재하지도 않고, 매우 큰 수에 대해 진행하는 소인수 분해는 계산적으로 너무 오래 걸린다.
RSA 암호의 문제점
부채널 공격(Side Channel Attack)
암/복호화 시에 비트 연산의 차이로 나타나는 규칙성으로 인해 시간차 공격 및 전력차 공격이 가능하다.
c.f.
지수연산이기에 지수 계산의 규칙성을 분석할 수 있다.
지수 승 계산시에 사용되는 전력 패턴의 차이를 분석한다 (1,0으로만 이루어져 있기 때문.)
이를 통해 priavte key에 대한 정보를 얻을 수 있다.
공개된 정보 : C(암호문), n(p*q값)
을 바탕으로 복호화시
C^(?) mod n = P
이기에 패턴을 통해 ?를 유추하기 쉽다
Deterministic 알고리즘
RSA는 이론상으로만 완벽하다.
하지만 deterministic하다는 문제점이 있다.
- same input -> same output!
일상생활에서 쓰려면 랜덤성을 부염해야 한다.
(대칭키 암호의 운영모드처럼!)
이는 OAEP(Optimal Asymmetric Encryption Padding)으로 해결된다.
OAEP

$P1\ ||\ P2$
$P1 = (m||0^{k1})\bigoplus G(r)$
$P2 = H(P1)\bigoplus r$
$|P1| = k - k_{0}, |P2| = k_{0}$
난수가 해시함수를 통해 m비트의 랜덤 해시값이 된다.
이 해시값과 M에 대해 XOR 연산을 수행한다. -> P1
기존 난수 값과 Hash(P1)에 대해 XOR 연산을 수행한다. -> P2
그리고 그 값을 암호화하여 최종적으로 RSA에 랜덤성을 부여할 수 있다.
RSA암호 이용시 권고사항
- n의 비트는 적어도 (서명의 경우) 2048 비트가 되어야 함
- 서로 다른 두 소수 p와 q는 적어도 1024 비트 이상이 되어야 함
- 서로 다른 두 소수 p와 q가 너무 가까이 있는 소수를 선택하지 않는다
- n을 공통적으로 이용하지 않는다
- 공개키 e는 2^16+1 = 65537을 이용하거나 이와 가까이 있는 값을 이용한다
- binary로 봤을 때 1이 적어서 연산이 빠르고 $\phi(n)$과 서로소 관계이기만 하면 됨
- 어차피 $\phi$(n)이 다르기 때문에 d는 다 다르게 나옴
- 안전하면서 1이 최소화된 값 = 65537
- 개인키 d가 노출되었을 경우, 수신자는 반드시 공개키 n,e ,개인키 d를 교체해야함
- OAEP를 이용하자.
감사합니다.
Ref
보안프로그래밍(2023), 숭실대학교 소프트웨어학부 조효진 교수님
Beginning Cryptography with Java/David Hook/Wrox press/2005
'Security' 카테고리의 다른 글
| 메시지 인증 코드(MAC) (0) | 2023.10.03 |
|---|---|
| 대칭키 암호 시스템의 운영모드 (0) | 2023.10.03 |
| 대칭키 암호 시스템, DES와 AES (0) | 2023.10.02 |
| 대칭키 암호 시스템 (0) | 2023.10.02 |
| 메시지 변조 감지 코드(MDC) (0) | 2023.09.29 |