Intro
본 포스팅에서는 암호학적 해시 함수에 대해 다룬다.
암호학적 해시 함수란

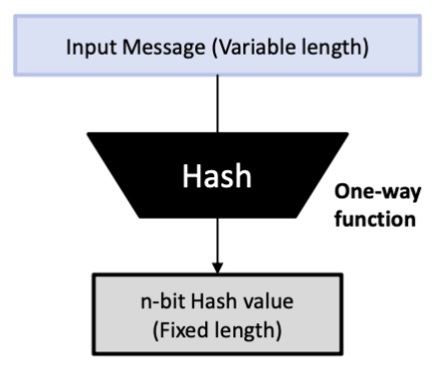
원본 메시지에 대해 고정된 크기의 출력을 하는 함수로서, 메시지에 대한 무결성을 보장해주기 위해 쓰인다.
다음과 같은 특징을 가진다.
임의의 크기의 데이터를 입력 값으로 가진다. (이론상 무한까지 가능)
고정된 크기의 출력 값으로 가진다.
- 보통 256비트 출력 값을 가진다.
- 공식적으로 정해진 양식들중에 가장 널리 사용되는 크기가 256비트이다. (called
SHA256)
하드웨어 및 소프트웨어의 적용이 쉬워야 한다.
어떤 입력 데이터에 대해서도 출력 값 계산하기 용이하다.
해쉬 함수는 공개된 함수이며 키가 사용되지 않는다.
키를 이용한 해쉬 함수 :
h = H(k,M)→MAC(메시지 인증코드)- 그러면 무결성, 인증 기능도 추가 된다.
암호학적 해쉬 함수는 공개키를 이용한 전자 서명을 생성하기 위하여 사용되기도 한다.
성능적으로 빠른 속도를 갖고 있기에 네트워크 스트리밍서비스 같은 곳에서 이용된다.
메시지 무결성
| 암호학적 해시 함수의 궁극적 목표
원본 메세지의 변조를 방지하기 위해 쓰인다.
대칭키 / 공개키 암호 시스템은 기밀성을 제공한다면, 암호학적 해시 함수는 무결성을 제공한다.
암호 시스템에서
MDC를 이용하여 무결성을 보장해준다.
MDC란?
메시지 변조 감지 코드로서, Modification Detection Code의 약자이다.
원본 메시지에 해시 함수를 적용시켜 MDC를 생성한다.
원본의 해시 값인 MDC와 수신한 메시지의 해시 값을 비교하여 허용되지 않은 사람이 메시지를 훼손했을 때 확인할 수 있다.
즉, 암호학적 해시 함수는 키가 없어 정보를 은닉할 수는 없지만 원본에 대한 훼손 및 변조 여부를 파악할 수 있다.
암호학적 해시 함수의 세 가지 성질
1. 역상 저항성(Preimage Resistance)
: Given h, infeasible to find x, s.t. H(x)=h
전자 지문이라고도 볼 수 있다.
등록된 지문을 보고 누구인지 유추 불가능한 것2. 제 2 역상 저항성(Second Preimage Resistance)
: Given x, infeasible to find y, s.t. H(y)=H(x)
등록된 지문을 보고, 이 지문과 같은 지문을 갖고 있는 사람을 찾는 것
전수조사 아니면 찾을 수가 없다.3. 충돌 저항성(Collision Resistance)
: infeasible to find any (x,y), s.t. H(y)=H(x)
모든 사람들 중 지문 같은 사람들을 찾는 것은 매우 어렵다.
즉, 무한의 정의역에서 치역이 일치하는 상황 발생인 것이다.
충돌상황을 찾기 어렵게 하는 것이 이 원리이다.제 2 역상 저항성(Second Preimage Resistance)에 대하여
- 이런 상황을 가정하자.
- X1 : Bob sends $5,000 to Alice
X2 : Bob transfer 5,000 won to Alice
IfH(X1) = H(X2), can we use a cryptographic hash function as a digital fingerprint? - 이런 의미 있는 두 문장들이 같은 값으로 나와버리면 어떻게 해야할까?
- 이런 충돌이 있을 수는 있지만 _유한한 시간_내에 의미있는 결과를 찾을 수 없다.
→ 이것이 해시 함수의 설계목적!
Avalanche Effect
암호학적 해시 함수의 대표적인 특징인 Avalanche Effect에 대해 알아보자.

암호학적 해시 함수는 위에서 설명한 3가지 성질을 모두 만족시키게끔 설계되었다.
그러다 보니 input 값이 1 bit라도 달라지게 되면 output은 완전히 달라지는 것이다.
암호학적 해시 함수의 설계 원리
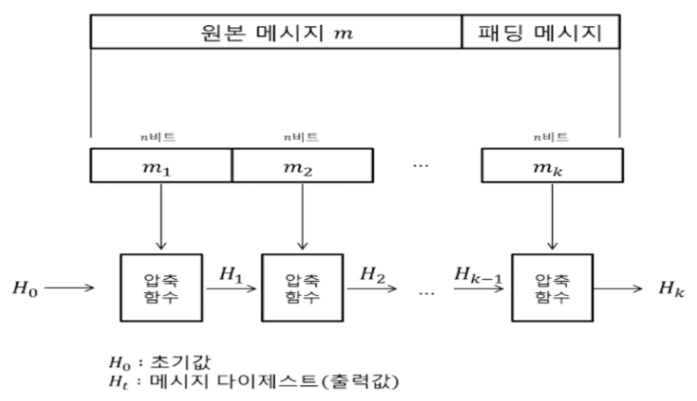
기본적으로 Merkle-damgard 구조를 가진다. (MD5, SHA-1, SHA-2 등)
원본 메시지 m과 패딩값을 concat한 data를 분할한다.분할할 떄, n bit의 배수가 되도록 한다.
$f(H_{0},m_{1}) = H_{1}$
- 초기 값 $H_{0}$, 압축함수 $f()$
- k번 수행하여 $H_k$를 생성 → h(m) = $H_k$
원본 메시지를 처리하는 블록의 단위(n bit)가 있다.
해당 단위로 원본 메시지를 처리하고, 남은 비트들은 패딩처리한다.
암호학적 해시 함수의 생일 문제 (Birthday Problems)

| 생일 문제란?
사람이 23명 모였을 때 생일이 같은 사람이 있을 사람이 있을 확률이 50% 이상이다.
→ 즉, 생각보다 적은 input 개수로도 output이 같을 확률이 생각보다 높다.
그러므로 충돌이 발생하는 확률이 output size에 비례하게 되어있음
$$
if\ output\ size = N, case\ of\ output = 2^N \ (bit)
$$
이에 암호학적 해쉬 함수를 아무리 잘 설계해도 256비트 일 때는 $2^{128}$ 개의 input만 준비하면 50%의 확률로 충돌되는 상황을 볼 수 있음
<자연적인 한계>
64비트 암호학적 함수 : 유한 시간내에 깨짐
160비트 암호학적 함수 : 유한 시간내에 이론상 깨짐
cf.
과거에는 64비트의 Output을 갖는 해쉬 함수가 안전하다고 판단되어 사용했으나
그러나 컴퓨터의 발달로 64비트 암호학적 해쉬 함수는 쉽게 충돌쌍을 찾을 수 있다.
즉, 언제나 기술의 발전으로 인해 암호 시스템이 무너질 수 있다.
암호학적 해시 함수의 활용
무결성 체크
- Storage
- data / H(Data)
- 하드디스크에 / 격리된 공간에 저장
- 디지털 포렌식
- 블록체인
- Data, H(Data) 데이터가 같이 담긴다.
- 프로그램 배포
- MDC (메시지 인증 코드)
- 전자서명
- 네트워크 통신
패스워드 관리
- Password
- 패스워드를 그대로 저장하기엔 보안상 안전하지 않기에 해시 값으로 저장한다. (with
salt) - 무결성 체크와는 다른 목적이다.
- 용량이 적기에 메모리 상 이점이 있다.
- 해시 값으로 저장되어 있기에 DB가 유출 되어도 안전하다.
- 사전 공격을 어느정도 막을 수 있다.
- 패스워드를 그대로 저장하기엔 보안상 안전하지 않기에 해시 값으로 저장한다. (with
감사합니다.
Ref
보안프로그래밍(2023), 숭실대학교 소프트웨어학부 조효진 교수님
Beginning Cryptography with Java/David Hook/Wrox press/2005
'Security' 카테고리의 다른 글
| 대칭키 암호 시스템 (0) | 2023.10.02 |
|---|---|
| 메시지 변조 감지 코드(MDC) (0) | 2023.09.29 |
| 보안 기본 개념 및 공격모델 (0) | 2023.09.26 |
| 정보보안의 이해 (0) | 2023.09.26 |
| About ARP Spoofing (1) | 2023.09.24 |